When I was a kid I loved making codes and still vividly remember my brother teaching me about simple substitution cyphers; I’d write messages and he’d then try to break them by looking for patterns and common letters like E to guess what offset I’d used. These were Ceasar Cyphers, or what in later life I would know as ROT13, where you shift each letter of the alphabet along by a certain number of letters. Both the sender and the recipient need to be using the same offset number, so some sort of prior communication is needed.
An offset of 3 would look like this:
ABCDEFGHIJ
DEFGHIJKLM
So A becomes encoded as D, B becomes E, C becomes F and so on.
I learned a hard lesson when my brother decoded one of my messages almost instantly. It turned out I’d left the plaintext message on the bottom of my code paper and hadn’t crossed it out well enough. He could still read it. ‘That’s not fair!’ I cried. ‘All’s fair in love and war’ came the reply. And indeed it was human errors like that that helped codebreakers in Bletchley Park break German World War 2 codes like Enigma. Many, many years later I taught a Year 5 lesson on the anniversary of D-Day in 2014 about codes and other things, and the same thing happened. One child caught another reading her plaintext. ‘That’s not fair!’ – which led to a discussion about the ethics of espionage in wartime.
So, everyone loves codes and cyphers, right? They make great coding activities as pairs of children can encode and decode secret messages whilst at the same time learning a bit of computer code, including how arrays, or ‘lists’, work in Scratch
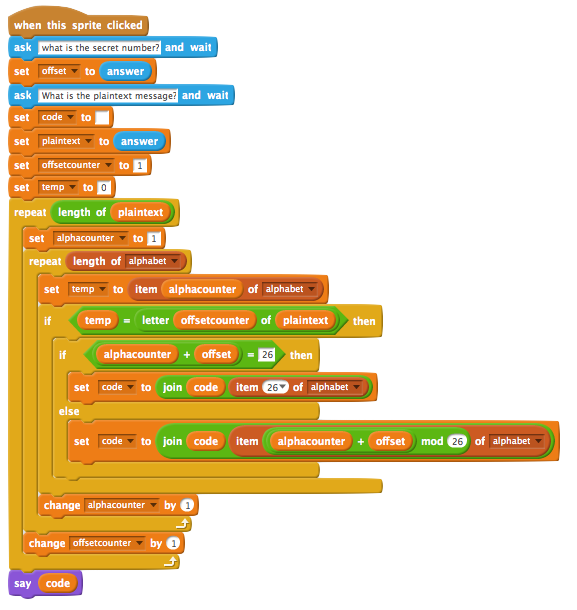
My first project is a really simple substitution cypher, a bit like ROT13, only you can choose any offset, not just 13. You click on a sprite and it asks you for the secret number – this is the offset, or how many letters along the alphabet each letter is going to be shifted.
Here’s how to use it: you click on Scratch cat to make a simple cypher that reverses your plaintext. You can use this a back slang generator (or decoder) – discover where the word ‘yob’ comes from!
Click on Nano on the top right to encode your plaintext message. You’ll be asked for the offset value (the ‘secret number’) and Nano will give you an encoded version of your message. You decode a message by giving it to Pico, in the middle. Note that if the offset is 13 you can use either Pico or Nano for encoding or decoding, but if you use any other number you’ll need to pick the right sprite for the job. (It doesn’t handle spaces or numbers – you might want to do that as an extension activity. If you do, you may think about whether spaces make your cypher easier to crack).
This is the code for the encoder:
This is how it works.
First it asks you what numerical offset you’d like to use, and puts this in a variable called offset. (There’s no error handling here if you type in 0 or letters – you might want to add that as an extension).
It then asks you for your plaintext message – the text you want to encode to keep it safe from prying eyes before sending it on. It puts your unencoded in a variable called plaintext.
You’ll then see a nested loop (a repeat loop within a repeat loop). The outer one repeats for the length of the message and keeps track of how far through the message it’s got using a variable called offsetcounter (which is a confusing name, I really need to change it). It does this to step through each character of the plaintext to analyse and encode it.
The inner loop runs 26 times (the length of the alphabet) for every character of the message. Each letter of the alphabet is held in a list (or array) called alphabet. It has to do this because, unlike some programming languages, I don’t think Scratch has an inbuilt way of turning text into numerical values. Nor do I think Scratch has a block that will find the numerical position of a given string in a list (though I may be wrong), which is why it has to test every character in the plaintext against the alphabet list to find that character’s numerical position in the alphabet, which is put in the alphacounter variable.
Each letter of the message is, in turn, put in a variable called temp. The code then runs through all 26 letters of the alphabet until it finds a match for the letter:
if (temp) = letter (offsetcounter) of (plaintext) then...
If this is true, we can get encoding!
The next line of code is quite complex, so let’s break it down.
We use the join block here. This is a string-handling block that allows you to glue text variables together. Our coded message is stored in a string (text variable) called code. Each time we encode a new letter we set the code string to be the message we’ve encoded so far, plus the new encoded character. That’s what the outer green join block does – look carefully how the colours overlap!
Let’s zoom in on the bit we’re adding each time:
item () of alphabet
is picking the coded letter from the alphabet, moving it on by the offset by picking item number alphacounter + offset. It’s a bit hard to see but there are two overlapping green blocks, one to do that adding, and another mod block.
Mod is short for modulo, or modular arithmetic. There’s an article on Nrich (that goes into way too much detail later on), and this really good article by Kalid Azad shows some great examples of why modular arithmetic is a useful trick to have up your sleeve: http://betterexplained.com/articles/fun-with-modular-arithmetic/
We need to use modular arithmetic for a couple of reasons. It’s best to think of our encoding not as sliding two lines of the alphabet along side each other (like I did at the top of the page), but as a circle (thank you tef):
This better shows what happens when you get to Z. What happens if I want to shift Z on by 3 letters? We cycle back round to the start again, so
TUVWXYZ
WXYZABC
So, with an offset of 3, Z in the plaintext becomes C in the encoded message.
Modular arithmetic also useful because I think it allows you to use offset numbers bigger than 26 – though they will be just the same as smaller numbers, but it helps avoid errors. Note that a secret number of 52 gives you the plaintext back again – why is this? Because 52 is twice 26. 52 mod 26 is zero, so you’re not doing any encoding at all!
The Scratch code is further complicated by the fact that there’s a special case when the encoded letter is Z. I’ll be honest, this was a bug I only spotted just as I was about to publish this and I ran the whole alphabet through it and noticed Z was missing from the coded message. If you encode WILL with an offset of 3, you should get ZLOO, but I was only getting LOO.
Useful debugging tips: display all your variables, add sounds like a drum and pauses inside loops to track what is going wrong. I found that the problem was caused when I was at the 26th letter of the alphabet (Z). 26 in modulo 26 is ZERO! And there’s no zeroth letter of the alphabet, so I catch this with
if alphacounter + offset = 26 then...
and manually set the encoded letter to z.
This is annoying because I had some reasonably elegant code, and now I have to test for a clunky exception right in the middle of it. Welcome to coding!
The decoder does the same process but in reverse.
Now this is fun, but it’s not a great cypher. It’s very easy to crack, partly because each letter is always encoded as the same letter making it possible to do frequency analysis if you have enough text to work on. The letter E is the most common letter in the English language, so if the most common letter in the coded text is J, you can be fairly sure that J is really E. That may suggest an offset of 5, you shunt all the other letters of the message back 5 places in the alphabet and see if the message makes sense.
Another flaw with substitution cyphers is that they allow you to spot patterns like double letters. If I encode the word HELLO using different offsets I get YVCCF or EBIIL or OLSSV. If you have an idea what the word may be, say a greeting at the start of a message, then that gives you a way in to breaking the code.
Which is why in the next session, we will make our code more cunning and harder to break by building a very simple Enigma machine in Scratch.