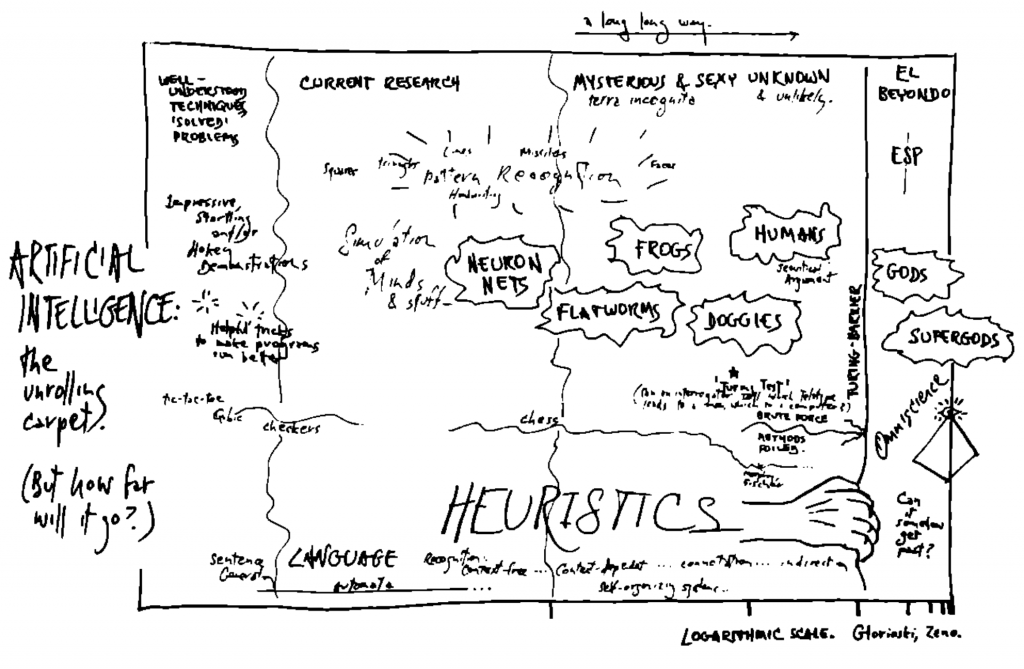
This is an unpublished article I wrote in around 1981 about a game my brother and I wrote for the Commodore PET. I am yet to find a program listing or cassette for the game, which I would love to spin up in a simulator! Incidentally, the Chris Howland mentioned in the article turns out to have quite an interesting life – born in Britain he became quite famous in Germany as a DJ, musician and actor.
After the initial novelty of having a computer in the house wore off, realising the limitations of the system (i.e. ‘IT’ wouldn’t wait on us hand and foot, answer the door, write best-selling war games) we thought about writing a good, solid, and maybe even an epic (-ette, -ish, sort of) program. Perhaps that was a mistake, but this is the story of our program, and how it was written. This is the story of SURIAS. A legend in its own FOR/NEXT loop.
Around the end of 1978 (yes, that long ago!), we (my brother Laurie, and myself) felt there was a lacking of interactive war games (except the infamous Star Trek) for the PET. This, of course, means the 2001 series (8k). We still have our old PET, and so this program runs in 8k, and was written in the old BASIC, although only two lines don’t work for new ROM PETs. A friend of Laurie, Andrew Shorney, who, by a meaningless coincidence, writes programs in COBOL for a supermarket chain, and himself, were in a pub getting rather drunk. (If there are any eligible Surias followers out there, it was the Naval Volunteer in Bristol). Andrew came up with the concept for the game. That was just the idea that you move armies from one county to another, and you have a stronghold, to which troops arrive by sea, and that the army of Surias has to defend its own country. You are, therefore, invading a country, in a time when the two opposing sides confronted each other on the battle field.
The name ‘Surias’ was invented, also, by Andrew (It’s an anagram of a certain large, well-known communist country). One evening Laurie told me the concept, but he couldn’t remember the name. “It’s an anagram of a large Communist country’: he said. A few minutes later I said “Surias?” I had re-discovered the name, and therefore claim a tiny fraction of the fame for the name. One Sunday, after lunch, Laurie took our PET over to Andrew’s house. By that evening the PET was back in our house with the map graphics on tape. Full credit for the graphics must go to Andrew, who before then, had never used a PET. Influenced by Chris Howland’s ‘Something Bit Me’ we began to try to write Surias.
That was a mistake.
A few days later: “We’re just being far too ambitious. It’s impossible”
Six months later. With the added knowledge of dimensioned variables (things like ?V(X) ) I decided it was possible to write Surias on our PET. Yes. Dimensioned variables, or as I call them, variable variables, they were the thing. In a few days time you could move troops, and it would print the numbers on the screen.
Now a few words to those thinking of writing a game on any computer, but especially the PET. A ‘Programmer’s Toolkit’ is very nice, and it makes life a lot easier, but it is not a necessity. To be honest, renumberers are necessary, but machine code versions on tape are just as good. Access to, or preferably ownership of, a printer is a huge help. We got our printer about halfway through the development. The toolkit came too late to be of much use.
Now back to the development. I put in the tests to check if there were enough armies in a particular county, and soon ‘Surias’ began to take shape.
Co-writing a program is a good idea. Many a time I would declare something impossible, returning a few minutes later only to find that Laurie had solved it.
Probably the biggest mistake we made, apart from starting on this whole venture in the first place:, was to structure the program badly. This is a direct result of not thinking how we would tackle each section of the program, in advance. I know that is the correct procedure, but those who are against letting a program take shape as it is written are probably the ones who stated a few years ago, that it was bad programming practice to use a ‘GOTO’ statement in a program. This may sound odd, but programming is more fun this way. Certainly, it is a lot less efficient, but programming becomes more of a pastime when done in this way. Heaven forbid, though, if people like Andrew wrote their COBOL programs that way!
There are many classics of space wasting in Surias. There are two different sections for winning and losing, with statements like “BATTLE IS UNDERWAY, SIR” being repeated. The table of POKE locations for the screen is repeated, but you need only enter it once, and change the line numbers for the second, or not at all, if you see the end of this article. These ‘faults’ are mainly due to the lack of a printer and toolkit when the main program was structured. The most useful toolkit function, apart from RENUMBER, we found to be FIND, which will find any variable, word, command, sentence, etc. in the whole program, and list it.
Soon the program was playable, and feeling pleased with ourselves, we showed it to my brother-in-law, saying we had just bought it from that PET orientated SOFTware house, for £5. He played a game, and remarked on what a bargain it had been. He now, of course, knows that we wrote it, and has a version running on his Nascom-1 under Xtal Basic. My other brother, Ashley, who has a KIM, has yet to implement Surias on his machine!
The program was left alone for some time, but then we started making little additions. The random sundry assorted disasters, for instance, or the summer and winter messages. One day we took our big box of software over to a friend’s house, Ken Otway, who looks exactly like the Tuscan designer on the cover of July 1980 Practical Computing. We showed him our latest version of the game. He gave us two very good ideas to improve it, incorperated in this version. One was to have battle reports being printed at the bottom of the screen, instead of the screen clearing every time. The other was to have something flashing on the screen where a battle is taking place. Should you be embarking on the process of writing a game, get as many people as possible to play it, and make suggestions.
The program is in no way intended to be at all historically accurate, or geographically correct.
February 1981: Shock! Horror! Bug Time
“Here,”said Laurie. “Get this American Cream Soda down you…you’re going to need it.”
I needed it. He had just discovered that if you capture counties 1-6 in any order, you won the game instantly. (Well as quickly as it takes to get counties 1-6). Bye bye, good times. Hello headaches.
April 1981: What was wrong with the program, is really rather embarrassing.
Many moons ago, when you could only hike through the galaxy on radio, I had this ace little routine that stopped any enemy armies accumulating in county 6, if you surrounded it. There was, however, a little snag…it didn’t work! Ho-hum. What could we do when inquisitive hackers asked what the routine did? “Oh yes,”came the reply. “That’s our fingerprint routine:” And there it remained. Infact, it was that, combined with line 550 being where 3395 is now, that messed it all up. The line to check if county 6 was lost had always read:
IF N(6)=0 THEN 1870
Due to friendly negative numbers popping up, we changed it to:
IF N (6)<=THEN 1870
...only going to prove that we're human, I suppose.
I hope you enjoy the game, and to save you thinking them out, here are some suggested alterations:
a) Give yourself more armies. (Line 270)
b) Give the PET fewer armies. (Line 310)
c) Make a 'disaster' less likely to happen. It stands at 1 in 20 at the moment. To make it, for instance, 1 in 50, change line 2170 so:
2170 PY=1:M0=51
Other possible refinements, if you have the memory, and/or money, could be CB2 sound, light pen (we've got one, but not enough memory to add the facility!), levels of difficulty, colour graphics, hi-res, and so on. Perhaps you might prefer "'Ark at they soldiers, sire:" in line 1520. There's no accounting for taste...
Thanks once again to Andrew Shorney, for thinking up the concept at Gateway's expense, and doing the map, Ken Otway, for helpful advice, and to Roger Horsman, for making us feel like well-known Pet Pundits. Also to Chris Howland, another 'calcaholic' like myself, and for giving us the sheer nerve to write a program.
