Inspired by http://www.sniff.org.uk/2015/12/hacking-pimoroni-flotillla.html I plugged Flotilla into my Mac. I browsed my /dev/ folder and took a guess that the Flotilla dock was ‘tty.usbmodem1421′ – which proved correct. Then I typed
screen /dev/tty.usbmodem1421 9600
at the Terminal prompt, and wiggled a few controls.
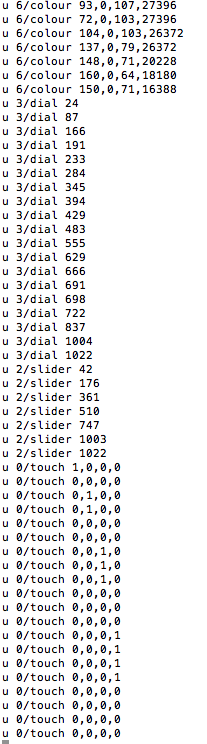
This is what I saw >
Straight away you can see values from named devices as I turned the dial and moved the slider. The 4 numbers on ‘touch’ seem to register 1 or 0 for each of the 4 buttons pressed, and the ‘colour’ values (judging from what I placed the colour sensor on) seem to be red, green, blue and overall brightness.
As per the Sniff article, I managed to get my LED strip to light red by typing
s 7 255,0,0
with the LEDs plugged into socket 1 on the dock – odd indeed that the port numbering is reversed.
I also managed to list all the devices that came with my Large Starter Kit by typing ‘d’ for debug:
# Debug information: # Resources: # SRAM free: 1362 bytes # Load: # Main loop duration: 6ms (0us) # Main loop cycles per second (fps): 148 # Channels: # 0 - weather (0x77) # 1 - motion (0x1d) # 2 - slider (0x16) # 3 - touch (0x2c) # 4 - dial (0x15) # 5 - matrix (0x60) # 6 - colour (0x29) # 7 - rainbow (0x54) u 0/weather 1964,101878 u 0/weather 1964,101883 u 0/weather 1964,101877
You can see some weather data there too – I thought this was pressure then temperature, but reading the Sniff article again I suppose it’s more likely to be 19.65 degrees C and 1018 millibars of air pressure.
Next step is to play with some proper OS X terminal software rather than using screen, and try to work out what parameters need passing to the LED matrix display – but looks promising that Flotilla can be made to work with other operating systems and computers aside from the Raspberry Pi.


did you go any further with this? interested in doing the same thing, since i don’t seem to be able to get raspbian to boot reliably.
Not yet – though Raspbian should boot reliably! Might be worth re-imaging the SD card or getting a new physical SD card? Any problems I’ve had booting before have been fixed that way.
Phil Howard from Pimoroni (a.k.a. Gadgetoid) has documented the ‘raw’ flotilla protocol in a gitbook here:
https://www.gitbook.com/book/gadgetoid/flotilla-protocol/details
He missed the brightness parameters for the matrix and number modules, but that’s a minor problem, everything else is documented.
Thank you Neil, I hadn’t seen that, most interesting!